Integrating Python with SwiftRNG
October 6, 2024
We’re excited to announce that our SwiftRNG Source Code Example documentation now includes a new Python sample code! This allows for direct integration with SwiftRNG using the device API.
This platform-independent example works on Windows, Linux and macOS, making it possible to utilize SwiftRNG in your projects.
More information about Python integration can be found at this location.
The latest SwiftRNG Software Kit can be downloaded at this address.
SwiftRNG as a RAND engine for openssl on Linux, FreeBSD and macOS
December 30, 2023
Today we are announcing an update to our SwiftRNG Software Kit API implementation.
With the latest version, a SwiftRNG device can act like a RAND engine and used with openssl command line tool.
This new feature is available on Linux, FreeBSD and macOS platforms.
More information about OpenSSL integration can be found at this location.
The latest SwiftRNG Software Kit can be downloaded at this address.
SwiftRNG Software Kit API implementation updates
July 21, 2023
Today we are announcing important updates to our SwiftRNG Software Kit API implementation. We have ported the API implementation logic, previously written in C, to C++. The new version of the software kit retains any previous APIs so that any existing applications, written in C and other languages, may require very little or no changes at all to continue functioning. The new API implementation also makes it possible for C++ applications to interface the API through provided C++ interface.
The latest SwiftRNG Software Kit can be downloaded at this location
Source code examples can be found at this address
AlphaRNG Software Kit now includes a C wrapper API
July 7, 2023
Announcing an addition to the AlphaRNG Software Kit that now includes a C wrapper API around the C++ API.
Applications written in C language can now communicate with an AlphaRNG device using AlphaRngApiCWrapper.c.
The new C wrapper serves as a bridge between C programs and the C++ API.
C examples using the C wrapper can be found at this address.
The latest AlphaRNG Software Kit that can be downloaded at
this location
SwiftRNG version update
March 26, 2023
We are happy to announce a version update for the SwiftRNG device. We are now shipping SwiftRNG version 1.4, which is fully compatible with SwiftRNG Software Kit and it is interchangeable with previous versions of SwiftRNG. The new version has an improved power consumption profile, it draws no more than 200 mA (depending on the selected power profile) in active mode and 80 mA when inactive. SwiftRNG now implements secure booting from an encrypted firmware image.
AlphaRNG SHA entropy extractors
October 2, 2022
In August we added alternative SHA-256 and SHA-512 entropy extractors to the AlphaRNG Software Kit. New SHA-256 and SHA-512 entropy extractors comply with NIST SP 800 90B section 3.1.5.1 (Recommendation for the Entropy Sources Used for Random Bit Generation) and NIST FIPS PUB 180-4 (Secure Hash Standard). The SHA entropy extraction logic is implemented into the software kit by applying SHA-512 or SHA-256 method to concatenated RAW random bytes of both noise sources retrieved from an AlphaRNG device. The SHA input/output extraction ratio used is 2/1, so that for each bit of extracted entropy there are two bits of raw data used as input.
The following describes how the SHA extraction was implemented.
Let NS1t be a raw random sample byte obtained as a result of digitizing the analog electrical noise of the first noise source at moment in time t.
Let NS2t be a raw random sample byte obtained as a result of digitizing the analog electrical noise of the second noise source at moment in time t.
Let RAWt be a raw random 16 bit number as a result of concatenation of bytes NS1t and NS2t at moment in time t so that:
RAWt = NS1t || NS2t
The raw input data used by SHA extractor is computed as following:
RAWnin = { RAWt1, RAWt2, RAWt3, … RAWtN }
where:
RAWnin - RAW bits used as input for the SHA method.
nin - number of bits used as input: 512 when using SHA-256 and 1024 when using SHA-512.
RAWt1 - a 16 bit raw number at moment in time t1 and e.t.c.
N - total amount of 16 bit raw numbers used as input for the SHA method: 256 when using SHA-256 and 512 when using SHA-512.
The final resulting entropy bits are computed as following:
outputnout = SHA ( RAWnin )
where:
nout - number of entropy bits in the output: 256 when using SHA-256 and 512 when using SHA-512.
The latest AlphaRNG Software Kit can be downloaded from the this address. More information about SHA extractors can be found at this location or here.
AlphaRNG Linux kernel module
August 7, 2022
We are happy to announce that a Linux kernel module alrandom is now available in the latest
AlphaRNG Software Kit.
The new module can be integrated into Linux kernel and act as a character Linux device.
Once the module is loaded then the random stream produced by an AlphaRNG device can be accessed
using /dev/alrandom device from within user space.
More information can be found at this location.
SwiftRNG LE is back in stock!
April 28, 2022
TectroLabs has not been immune to the global shortage of microchips and other components we use to assemble our hardware products. However, we are happy to announce that after securing additional supply, SwiftRNG LE is back in stock and will be in stock for the forseeable future.
Additionally, we are now shipping SwiftRNG LE version 1.4, which contains upgraded components. This version continues to be fully compatible with SwiftRNG Software Kit and is interchangeable with previous versions of SwiftRNG LE.
Visit our SwiftRNG page for more information on each SwiftRNG edition.
Linux swrandom driver updates to support latest SwiftRNG versions and models
January 24, 2022
We are announcing a major update to the swrandom Linux module/driver that adds support for SwiftRNG CDC/ACM devices.
The updated driver is compatible with all SwiftRNG versions and models and it can be used on Linux platforms with kernel versions such as 4.14 or newer.
Form more information about using swrandom Kernel module/driver please visit this address.
AlphaRNG and SwiftRNG Software Kits updates to support FreeBSD 13.
November 7, 2021
We have updates our Software Kits for SwiftRNG and AlphaRNG devices and added experimental support for FreeBSD. All of AlphaRNG and SwiftRNG devices, including older versions, can now be used with FreeBSD 13.
Latest AlphaRNG and SwiftRNG software kits require no additional components and can easily be used on FreeBSD 13 platform.
AlphaRNG quick start guide explains AlphaRNG software installation and verification steps for FreeBSD 13.
SwiftRNG quick start guide explains SwiftRNG software installation and verification steps for FreeBSD 13.
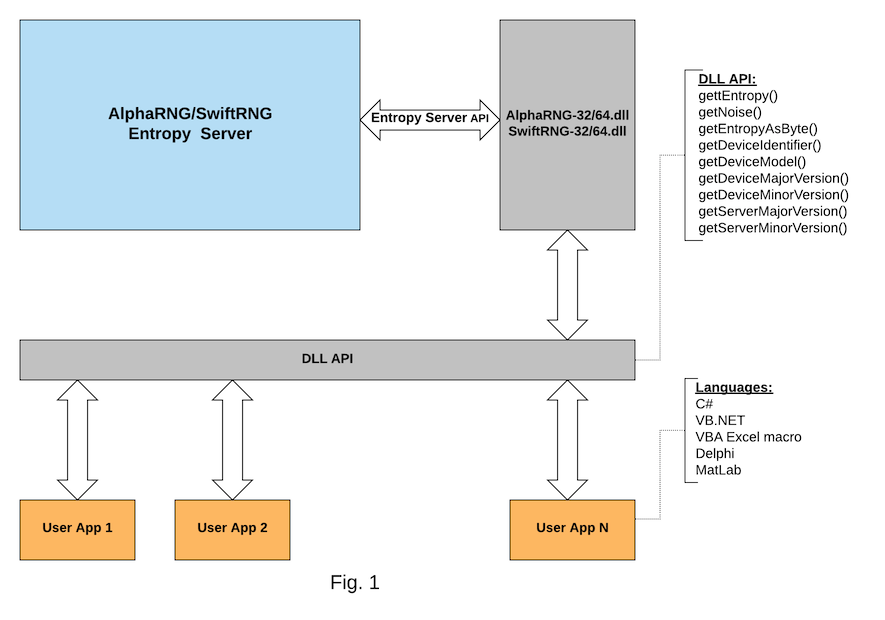
AlphaRNG and SwiftRNG entropy server API updates. New DLLs for entropy server connectivity.
July 11, 2021
We’re excited to announce new DLLs for AlphaRNG and SwiftRNG entropy servers. Our new DLLs simplify integration of applications using languages such as C#, VB, VBA Excel Macro, Delphi, MatLab with entropy servers on Windows 64-bit platforms.
Latest AlphaRNG and SwiftRNG software kits include updated copies of entropy servers and new SwiftRNG-32.dll, SwiftRNG-64.dll, AlphaRNG-32.dll and AlphaRNG-64.dll libraries.
The latest updates for the AlphaRNG Entropy Server API can be found at this location and the latest updates for the SwiftRNG Entropy Server API can be found at this location.
SwiftRNG Pro hardware and firmware updates
May 2, 2021
We have updated the SwiftRNG Pro version. The new 2.2 version consists of hardware and software enhancements for improving overall performance, power consumption and security. The new SwiftRNG Pro version is 100% compatible with the previous version and it is capable of providing true random numbers at 210 Mbps speed.
SwiftRNG Pro can be purchased through TectroLabs store or through Amazon store.
More information about SwiftRNG Pro can be found at this address.
Adding Windows support for AlphaRNG devices
March 22, 2021
With the new AlphaRNG Software Kit 2.0, we bring Windows support to AlphaRNG devices! The latest software kit can be downloaded at this location.
AlphaRNG devices can now be used with 64bit Windows 10 and with 64bit Windows Server 2016/2019. AlphaRNG quick start guide explains software requirements, installation and verification steps for Windows.
More information about Windows integration can be found at this address.
Introducing AlphaRNG: Our next-generation random number generator
February 8, 2021

Today, we are excited to announce AlphaRNG, our next-generation hardware random number generator. Much like SwiftRNG, AlphaRNG is a small, USB flash drive-sized device that can be used with Linux, Windows and macOS computers. However, where it excels is in its communication interface and enhanced reliability.
AlphaRNG implements data communications over a secure channel for confidentiality, integrity, and replay protection using a USB interface. We have also enhanced the design to ensure the reliability of the built-in health tests using a technique known as hardware fault insertion (also known as fault injection). Hardware fault insertion is used to create temporary signal faults in the noise sources for the purpose of validating the expected behavior of the device under failure conditions.
AlphaRNG can be integrated in software projects through the provided software API implementation kit and software utilities. Thanks to the small physical dimensions and light weight, AlphaRNG may be placed inside a computer enclosure and connected via an internal USB port. It can also be connected directly to any external USB port and used over a secure communication channel.
We hope that you’ll consider AlphaRNG for generating true random numbers using a secure channel. It can be purchased starting today here, and full information is available on the main AlphaRNG page.
Announcing a refresh to SwiftRNG lineup
April 3, 2020
Today we are pleased to announce a refresh to our SwiftRNG lineup. This new lineup consists of SwiftRNG version 1.3, SwiftRNG Pro version 2.1, SwiftRNG version 1.3 and SwiftRNG Z version 3.1.
The new lineup consist of enhancements that address USB interface compatibility with certain operating systems when used in virtual computing environment.
Our latest versions of SwiftRNG devices are compatible with Linux, macOS, Windows 10 (64 bit) and Windows Server 2016/2019 (64 bit) and can be used with virtual machine software such as VMware Player, VMware ESXi, VirtualBox and Parallels.
These SwiftRNG devices require using the latest version of the SwiftRNG Software API kit, which can be downloaded here.
Announcing MicroRNG
November 24, 2019

Another day, another product! Today we’re announcing a true random number generator in a new form: mikroBUS™, which is the world’s fastest growing add-on board standard. Aptly, we’re calling this new device the MicroRNG.
The TectroLabs MicroRNG is a hardware (true) random number generator device that can be used in embedded systems as a reliable entropy source. It can interface with microcontrollers or microprocessors (mainboards) with integrated circuits and modules through a mikroBUS socket. Generated random numbers can be retrieved from a MicroRNG through an API that is implemented over an SPI interface or a 2-wire UART interface.
MicroRNG can generate random numbers at a rate up to 1 Mbps in SPI mode and up to 1.5 Mbps in UART mode. It embeds comprehensive diagnostics and monitoring features used for validating internal random physical sources and components in real-time. It also maintains an internal status, which can be retrieved using the device API to check the health of the generator.
MicroRNG can be purchased today at our online shop for $179 USD. Learn more on the MicroRNG page, or go directly to the datasheet PDF.
Entropy Server API exposed
October 26, 2019
A new documentation section has been created to expose the API that is implemented in the Windows Entropy Server.
It will help existing users and developers better understand how Entropy Server works in order to shorten their development
and implementation efforts. Applications written in languages such as C/C++, C#, Java, Delphi can concurrently retrieve
true random bytes generated by SwiftRNG devices by directly connecting with the entropy-server.
For source code examples visit this address.
More information about the API can be found at this location.
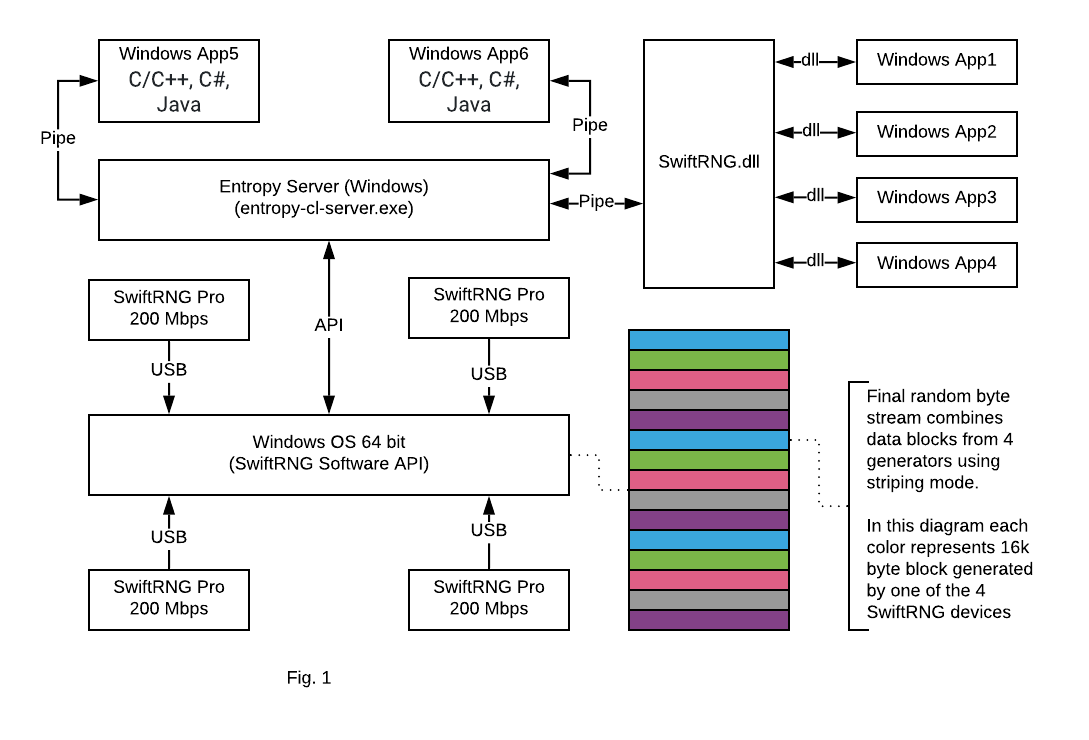
Cluster capability of Entropy Server with 64 bit Windows
April 10, 2019
We are announcing today an important update of the SwiftRNG Software Kit. Beginning with version 4.5, the SwiftRNG API contains device cluster scalability and fail-over capabilities for 64-bit Windows. This makes it possible to use multiple SwiftRNG devices to increase the total random number generation speed. This new API feature seamlessly integrates multiple devices on Windows and uses them concurrently as a single stream of random numbers.
The software update comes with a new entropy-cl-server.exe, which is a Windows based pipe server
that uses a duplex-named pipe for distributing random bytes generated by two or more SwiftRNG devices.
Windows applications can concurrently access entropy-cl-server through the provided SwiftRNG.dll.
Applications written in languages such as C/C++, C#, and Java can concurrently retrieve true random bytes generated by a cluster of SwiftRNG devices by connecting with the entropy-cl-server directly through the named pipe.
Source code examples are available
here.
In this post, we will show how to use four SwiftRNG Pro devices to generate a high quality random number stream at a speed of 800 Mbps (Fig. 1).
We recommend the following computer hardware configuration for testing:
- A fast CPU, with at least 6 logical processors. (We used an I7-3630QM CPU @ 2.4 GHz.)
- 4 USB highspeed ports. USB 3 type is recommended for best results. (We used a Toshiba Satellite Laptop P878-S7102.)
- Windows 10 64-bit
- Four SwiftRNG Pro devices: each device should be plugged directly into a USB port. Do not use USB hubs.
entropy-cl-server.exeavailable from a command line.
To test your SwiftRNG Pro device cluster performance, start entropy-cl-server.exe by entering the following in the command line:
entropy-cl-server.exe -cs 4
The output may look like this:
Entropy server started using a cluster of 4 devices, post processing: 'default', on named pipe: \\.\pipe\SwiftRNG
Open a new command line window and enter the following:
entropy-client-test.exe
The output may look like this:
----------------------------------------------------------------------------
-------------------------- entropy-client-test -----------------------------
--- A program utility for testing the connectivity to the entropy server. --
--- Usage: entropy-client-test [pipe endpoint] -----------------------------
----------------------------------------------------------------------------
Using named pipe: \\.\pipe\SwiftRNG
-------- Testing connectivity to the entropy server using named pipes ------
Connecting to the entropy server pipe .............................. SUCCESS
Retrieving 100000 bytes from the entropy server .................... SUCCESS
Running pipe communication diagnostics ............................. SUCCESS
Calculating entropy download speed ................................. 800.00 Mbps
------------ Testing connectivity to the entropy server using DLL ----------
Loading SwiftRNG.dll ............................................... SUCCESS
Getting proc addr swftSetEntropyServerPipeEndpointSynchronized() ... SUCCESS
Calling swftSetEntropyServerPipeEndpointSynchronized() ............. SUCCESS
Getting proc address swftGetByteFromEntropyServerSynchronized() .... SUCCESS
Testing swftGetByteFromEntropyServerSynchronized() ................. SUCCESS
swftGetByteFromEntropyServerSynchronized() download speed .......... 266.67 Mbps
Testing swftGetByteFromEntropyServerSynchronized() 50 threads ----- SUCCESS
Getting proc address swftGetEntropyFromEntropyServer() ............. SUCCESS
swftGetEntropyFromEntropyServer() download speed ................... 800 Mbps
Announcing SwiftRNG Z — A Zener breakdown-based true random number generator
March 23, 2019

Today we are excited to announce a new device in the SwiftRNG family. Introducing SwiftRNG Z, a random number generator based on Zener breakdown effect (due to quantum tunneling). SwiftRNG Z is a USB stick-sized device that generates random numbers at a rate of 80 megabits per second. Backwards compatible with SwiftRNG, SwiftRNG Pro and SwiftRNG LE, it can be used with Linux, macOS and Windows.
SwiftRNG Z fits a wide range of uses, including research, simulations, and generating secure session and encryption keys.
SwiftRNG Z can be purchased at our online shop for $349. Learn more on the SwiftRNG Z page. Full documentation is available online.
Entropy Sector API Live Demos
March 10, 2019
We have created a demo website that showcases the usage of our Entropy Sector API (ESAPI). The ESAPI can be used to quickly retrieve true random numbers from a live stream of random numbers that are being generated by a SwiftRNG.
The first demo uses the ESAPI to simulate the result of a coin flip. The second demo simulates a roll of three dice. Each time you flip the coin or roll the dice, your browser makes a call to the API to retrieve random numbers. These demos were built using JavaScript and React, and the source code is available here.
Announcing the TectroLabs education discount
September 9, 2018
With the fall semester in full swing in many universities this week, we are happy to announce that starting today, students and educators can save 20% on all SwiftRNG purchases! Visit our education discount page to learn about who qualifies, and how to receive this discount.
SwiftRNGs are versatile random number generators that are compatible with Windows, macOS, and Linux. Designed to pass top statistical tests for randomness, including Diehard, Dieharder, and NIST, they can be used for a wide variety of academic purposes.
Using ‘bitcount’ to test a SwiftRNG Pro cluster with a 2 Gbps generation speed
August 25, 2018
In one of our previous blog posts, we showed you how to build a cluster of five SwiftRNG Pro devices to achieve a random number generation speed of 1 Gbps of. In this post, we will demonstrate how to measure the speed and verify the quality of random bits produced by a cluster of ten SwiftRNG Pro devices.
For best results, your host machine should meet or exceed the following specifications:
- A fast CPU with at least 6 cores. (We used a six core I7-8700 CPU at 3.2 GHz.)
- A mainboard that supports at least 10 USB high-speed ports (USB 3.0 is recommended). We used a ‘Gigabyte Ultra Durable Motherboard Z370 HD3P LGA 1151’.
- Cent OS 7.
- 10 SwiftRNG Pro devices — each device should be plugged directly into an available USB port. No USB hubs should be used in between.
- SwiftRNG software utilities are built and available for CentOS from a command line. Please visit this address for specific details.
Verify that all ten SwiftRNG Pro devices are ready and accessible by entering the following in the command line:
swrng -ld
The output may look like this:
{DevNum=0 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=26AB737E1C09D20}
{DevNum=1 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=A8258CD5FE7B964}
{DevNum=2 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=7F68712D6D6EB12}
{DevNum=3 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=C73785CD7552FCD}
{DevNum=4 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=C1890C098FB1B92}
{DevNum=5 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=F36D8EA26BA7522}
{DevNum=6 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=52CB6954F44C84E}
{DevNum=7 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=66E05DA74F52BDE}
{DevNum=8 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=B2C27DB40F2409A}
{DevNum=9 DevModel=SWRNGPRO DevVer=V2.0 DevS/N=2B2EE4AFBB420F8}
Verify the cluster generation speed is at 2 Gbps by entering the following in the command line:
swperf-cl-test 10
The output may look like this:
------------------------------------------------------------------------
-- swperf-cl-test - SwiftRNG device cluster performance test utility --
------------------------------------------------------------------------
Cluster preferred size: 10, actual cluster size: 10 (successfully open)
Setting power profiles to 9 ------------------------------- Success
Post processing ---( for devices with version 1.2+ )----- disabled
Performance ------- in progress ------------------ 2000.00 Mbits/sec
Post processing ------------------------------------------- SHA256
Performance ------- in progress ------------------ 1333.33 Mbits/sec
Post processing ------------------------------------------- SHA512
Performance ------- in progress ------------------ 2000.00 Mbits/sec
Post processing ---( for devices with version 1.2+ )--- xorshift64
Performance ------- in progress ------------------ 2000.00 Mbits/sec
Closing device -------------------------------------------- Success
Available for Windows, macOS and Linux, bitcount is a utility that can be used to count the number of 0 and 1 bits
in a random byte stream generated by a SwiftRNG device for quality verification. An ideal generator will produce an equal amount of 0 and 1 bits over a period of time; however that is rarely achievable when
using real random number generators.
We will use bitcount-cl utility (a cluster version of bitcount) for calculating arithmetic mean of zeroes among all of the random bytes generated by the SwiftRNG Pro cluster. The following command demonstrates how to count 1 and 0 bits for 75,000,000 random blocks (about 1 TB) retrieved from a SwiftRNG Pro cluster (one block equals to 16,000 bytes):
bitcount-cl 75000000 10
This could result in the following output (it will take around 90 minutes to get results):
---------------------------------------------------------------------------------
--- A program for counting 1's and 0's bits retrieved from a SwiftRNG cluster ---
---------------------------------------------------------------------------------
SwiftRNG cluster of 10 devices open successfully
*** downloading random bytes and counting bits using 'default' post processing method ***
retrieved 9600000000000 total bits, 0's bit count: 4800000240406, 1's bit count: 4799999759594, 0's arithmetic mean: 0.500000025
In the output shown above, you will notice a discrepancy between 0 and 1 counts. The cluster produced more 0 bits than 1 bits, however that discrepancy is small and can be ignored. A tiny amount of bias or a small error in random sources would have resulted in a huge discrepancy in counts for 1 terabyte of random data.
Let’s run the same bitcount-cl test several times and record the resulting statistics in a table.
We may end up with the following:
| Total bits sampled | number of bits with 0 values | number of bits with 1 values | 0's arithmetic mean |
| ------------------ | ---------------------------- | ---------------------------- | -------------------- |
| 9600000000000 | 4799999080595 | 4800000919405 | 0.499999904 |
| 9600000000000 | 4800001980675 | 4799998019325 | 0.500000206 |
| 9600000000000 | 4799999260118 | 4800000739882 | 0.499999923 |
New Utility: Entropy Pool Feeder for Linux
July 2, 2018
This past month, we launched a new open source utility for Linux called Entropy Pool Feeder (epf). In Linux, the entropy pool is used as a source of high quality randomness for a variety of security operations. The entropy pool is accessed using the /dev/random device. To avoid entropy pool starvation, it is important to maintain the pool with enough randomness.
The epf utility can be used to properly maintain the pool, by continuously monitoring the entropy pool, and feeding it with a high quality true randomness when the entropy level is below the threshold value. The randomness can be securely downloaded from a remote service such as entropysector.com.
Visit the Entropy Pool Feeder repository on GitHub to learn how to use this utility, and to download the source code. You can also visit the latest release to quickly get the latest version.
Introducing Entropy Sector API
June 23, 2018
Entropy Sector API is an application service that makes SwiftRNG true randomness available to your application using RESTful API. The new API is deployed to https://entropysector.com and it is accessible from any application with an internet connection.
A commercial version of the API will be available later this year. Our Entropy Sector API documentation provides information to get started with the service.
Comparing SwiftRNG Pro with /dev/urandom
May 12, 2018
The purpose of this posting is to test and compare the quality of the random numbers generated by a SwiftRNG Pro device and those generated by PRNG (pseudorandom number generator) implementations available on Linux operating systems. In Linux-like operating systems, /dev/urandom is a special file that serves as a PRNG.
For our tests we used a /dev/urandom file available on a computer running CentOS 7 and a SwiftRNG Pro device plugged into one of the USB ports available on the same computer. The tests were performed by sampling 120 GB of random data from SwiftRNG Pro device with no ‘conditioning’ and from /dev/urandom. The sampled random data blocks were used to feed the ‘rngtest’ test suite for statistical analysis. We also tested SwiftRNG Pro and /dev/urandom random streams using the ‘dieharder’ test suite.
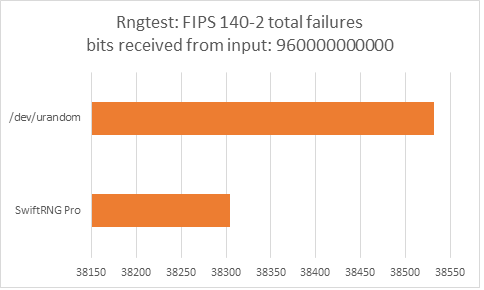
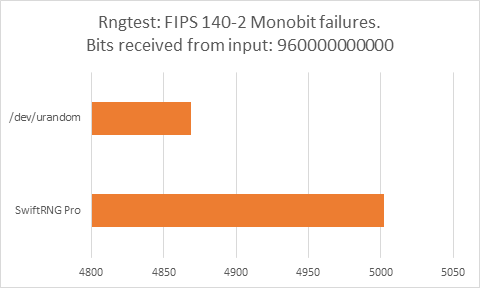
Testing with ‘rngtest’
The following charts represent comparison test results produced by ‘rngtest’. We are interested in the total number of FIPS 140-2 test failures and number of failures for each FIPS 140-2 specific test.
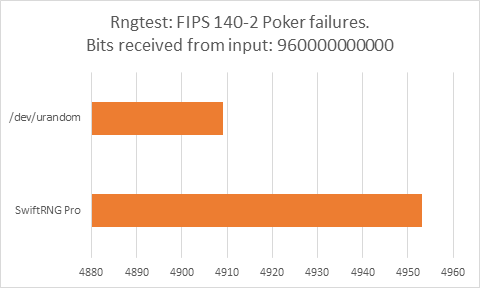
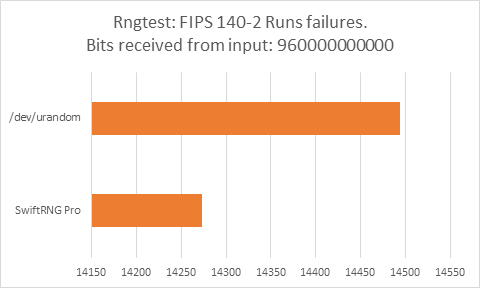
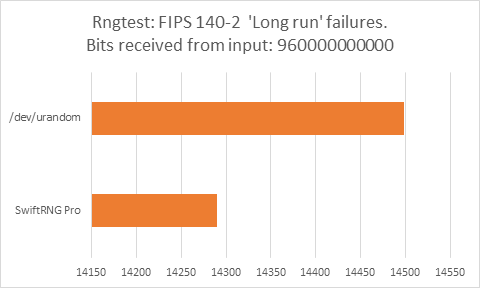
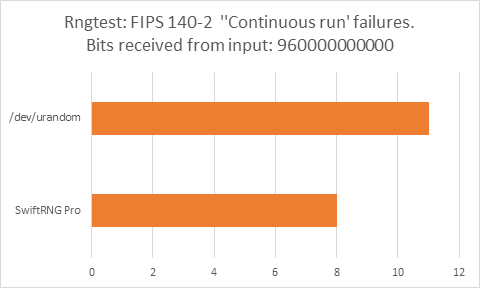
‘rngtest’ Conclusion
The total number of FIPS 140-2 failures was slightly higher for /dev/urandom compared to FIPS 140-2 failures for SwiftRNG Pro. SwiftRNG Pro produced less failures for FIPS 140-2 ‘Runs’, ‘Long Run’ and ‘Continuous Run’ tests while /dev/urandom produced less failures for FIPS 140-2 ‘Monobit’ and ‘Poker’ tests.
Testing with ‘dieharder’
The following are test results generated by ‘dieharder’ when testing random byte stream produced by SwiftRNG Pro device with no ‘conditioning’:
swrng -dd -fn STDOUT | dieharder -g 200 -a
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name |rands/second| Seed |
stdin_input_raw| 5.52e+06 | 204447751|
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
diehard_birthdays| 0| 100| 100|0.23189457| PASSED
diehard_operm5| 0| 1000000| 100|0.75095612| PASSED
diehard_rank_32x32| 0| 40000| 100|0.96073461| PASSED
diehard_rank_6x8| 0| 100000| 100|0.93232326| PASSED
diehard_bitstream| 0| 2097152| 100|0.32747213| PASSED
diehard_opso| 0| 2097152| 100|0.74231200| PASSED
diehard_oqso| 0| 2097152| 100|0.09245298| PASSED
diehard_dna| 0| 2097152| 100|0.30959114| PASSED
diehard_count_1s_str| 0| 256000| 100|0.86246827| PASSED
diehard_count_1s_byt| 0| 256000| 100|0.33426616| PASSED
diehard_parking_lot| 0| 12000| 100|0.33358085| PASSED
diehard_2dsphere| 2| 8000| 100|0.45323736| PASSED
diehard_3dsphere| 3| 4000| 100|0.68247073| PASSED
diehard_squeeze| 0| 100000| 100|0.04045060| PASSED
diehard_sums| 0| 100| 100|0.15998991| PASSED
diehard_runs| 0| 100000| 100|0.20507955| PASSED
diehard_runs| 0| 100000| 100|0.81059682| PASSED
diehard_craps| 0| 200000| 100|0.04558382| PASSED
diehard_craps| 0| 200000| 100|0.45402435| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.62754383| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.53365537| PASSED
sts_monobit| 1| 100000| 100|0.07245620| PASSED
sts_runs| 2| 100000| 100|0.49969326| PASSED
sts_serial| 1| 100000| 100|0.50668731| PASSED
sts_serial| 2| 100000| 100|0.87844642| PASSED
sts_serial| 3| 100000| 100|0.99987535| WEAK
sts_serial| 3| 100000| 100|0.96930487| PASSED
sts_serial| 4| 100000| 100|0.50879386| PASSED
sts_serial| 4| 100000| 100|0.22925809| PASSED
sts_serial| 5| 100000| 100|0.41114562| PASSED
sts_serial| 5| 100000| 100|0.85418243| PASSED
sts_serial| 6| 100000| 100|0.52907030| PASSED
sts_serial| 6| 100000| 100|0.79775328| PASSED
sts_serial| 7| 100000| 100|0.25207091| PASSED
sts_serial| 7| 100000| 100|0.45934295| PASSED
sts_serial| 8| 100000| 100|0.44472162| PASSED
sts_serial| 8| 100000| 100|0.54690406| PASSED
sts_serial| 9| 100000| 100|0.75462311| PASSED
sts_serial| 9| 100000| 100|0.59246043| PASSED
sts_serial| 10| 100000| 100|0.65093398| PASSED
sts_serial| 10| 100000| 100|0.36015871| PASSED
sts_serial| 11| 100000| 100|0.83071639| PASSED
sts_serial| 11| 100000| 100|0.99480125| PASSED
sts_serial| 12| 100000| 100|0.88728666| PASSED
sts_serial| 12| 100000| 100|0.84685621| PASSED
sts_serial| 13| 100000| 100|0.44996132| PASSED
sts_serial| 13| 100000| 100|0.84783628| PASSED
sts_serial| 14| 100000| 100|0.54973990| PASSED
sts_serial| 14| 100000| 100|0.98901587| PASSED
sts_serial| 15| 100000| 100|0.92734287| PASSED
sts_serial| 15| 100000| 100|0.74516197| PASSED
sts_serial| 16| 100000| 100|0.65420669| PASSED
sts_serial| 16| 100000| 100|0.91095922| PASSED
rgb_bitdist| 1| 100000| 100|0.28196469| PASSED
rgb_bitdist| 2| 100000| 100|0.20311887| PASSED
rgb_bitdist| 3| 100000| 100|0.83371006| PASSED
rgb_bitdist| 4| 100000| 100|0.97918552| PASSED
rgb_bitdist| 5| 100000| 100|0.33633146| PASSED
rgb_bitdist| 6| 100000| 100|0.45049719| PASSED
rgb_bitdist| 7| 100000| 100|0.84676874| PASSED
rgb_bitdist| 8| 100000| 100|0.18405803| PASSED
rgb_bitdist| 9| 100000| 100|0.17870007| PASSED
rgb_bitdist| 10| 100000| 100|0.34093733| PASSED
rgb_bitdist| 11| 100000| 100|0.98757745| PASSED
rgb_bitdist| 12| 100000| 100|0.33608530| PASSED
rgb_minimum_distance| 2| 10000| 1000|0.40714300| PASSED
rgb_minimum_distance| 3| 10000| 1000|0.01359258| PASSED
rgb_minimum_distance| 4| 10000| 1000|0.40526430| PASSED
rgb_minimum_distance| 5| 10000| 1000|0.00015977| WEAK
rgb_permutations| 2| 100000| 100|0.42947333| PASSED
rgb_permutations| 3| 100000| 100|0.70231583| PASSED
rgb_permutations| 4| 100000| 100|0.14559228| PASSED
rgb_permutations| 5| 100000| 100|0.39820769| PASSED
rgb_lagged_sum| 0| 1000000| 100|0.95478426| PASSED
rgb_lagged_sum| 1| 1000000| 100|0.48808137| PASSED
rgb_lagged_sum| 2| 1000000| 100|0.75232711| PASSED
rgb_lagged_sum| 3| 1000000| 100|0.30510638| PASSED
rgb_lagged_sum| 4| 1000000| 100|0.32466480| PASSED
rgb_lagged_sum| 5| 1000000| 100|0.34657161| PASSED
rgb_lagged_sum| 6| 1000000| 100|0.79797715| PASSED
rgb_lagged_sum| 7| 1000000| 100|0.69093277| PASSED
rgb_lagged_sum| 8| 1000000| 100|0.62220023| PASSED
rgb_lagged_sum| 9| 1000000| 100|0.75880907| PASSED
rgb_lagged_sum| 10| 1000000| 100|0.60912315| PASSED
rgb_lagged_sum| 11| 1000000| 100|0.68534716| PASSED
rgb_lagged_sum| 12| 1000000| 100|0.56160475| PASSED
rgb_lagged_sum| 13| 1000000| 100|0.50051735| PASSED
rgb_lagged_sum| 14| 1000000| 100|0.03065363| PASSED
rgb_lagged_sum| 15| 1000000| 100|0.46737147| PASSED
rgb_lagged_sum| 16| 1000000| 100|0.96676303| PASSED
rgb_lagged_sum| 17| 1000000| 100|0.63337053| PASSED
rgb_lagged_sum| 18| 1000000| 100|0.62142304| PASSED
rgb_lagged_sum| 19| 1000000| 100|0.04809293| PASSED
rgb_lagged_sum| 20| 1000000| 100|0.71276787| PASSED
rgb_lagged_sum| 21| 1000000| 100|0.78284283| PASSED
rgb_lagged_sum| 22| 1000000| 100|0.39360698| PASSED
rgb_lagged_sum| 23| 1000000| 100|0.06632147| PASSED
rgb_lagged_sum| 24| 1000000| 100|0.79035290| PASSED
rgb_lagged_sum| 25| 1000000| 100|0.22745596| PASSED
rgb_lagged_sum| 26| 1000000| 100|0.98940777| PASSED
rgb_lagged_sum| 27| 1000000| 100|0.59552952| PASSED
rgb_lagged_sum| 28| 1000000| 100|0.76529954| PASSED
rgb_lagged_sum| 29| 1000000| 100|0.96033546| PASSED
rgb_lagged_sum| 30| 1000000| 100|0.34793801| PASSED
rgb_lagged_sum| 31| 1000000| 100|0.56710980| PASSED
rgb_lagged_sum| 32| 1000000| 100|0.87580841| PASSED
rgb_kstest_test| 0| 10000| 1000|0.59457755| PASSED
dab_bytedistrib| 0| 51200000| 1|0.26956602| PASSED
dab_dct| 256| 50000| 1|0.43445042| PASSED
Preparing to run test 207. ntuple = 0
dab_filltree| 32| 15000000| 1|0.95997359| PASSED
dab_filltree| 32| 15000000| 1|0.69594477| PASSED
Preparing to run test 208. ntuple = 0
dab_filltree2| 0| 5000000| 1|0.69858902| PASSED
dab_filltree2| 1| 5000000| 1|0.76921713| PASSED
Preparing to run test 209. ntuple = 0
dab_monobit2| 12| 65000000| 1|0.85449699| PASSED
The following are test results generated by ‘dieharder’ when testing random byte stream produced by /dev/urandom:
dd if=/dev/urandom bs=12000000 | dieharder -g 200 -a
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name |rands/second| Seed |
stdin_input_raw| 3.06e+07 |2868936241|
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
diehard_birthdays| 0| 100| 100|0.95387771| PASSED
diehard_operm5| 0| 1000000| 100|0.92560719| PASSED
diehard_rank_32x32| 0| 40000| 100|0.98066045| PASSED
diehard_rank_6x8| 0| 100000| 100|0.20597070| PASSED
diehard_bitstream| 0| 2097152| 100|0.91045462| PASSED
diehard_opso| 0| 2097152| 100|0.63316244| PASSED
diehard_oqso| 0| 2097152| 100|0.93774044| PASSED
diehard_dna| 0| 2097152| 100|0.41448575| PASSED
diehard_count_1s_str| 0| 256000| 100|0.57649363| PASSED
diehard_count_1s_byt| 0| 256000| 100|0.10827822| PASSED
diehard_parking_lot| 0| 12000| 100|0.79252967| PASSED
diehard_2dsphere| 2| 8000| 100|0.04975508| PASSED
diehard_3dsphere| 3| 4000| 100|0.99585638| WEAK
diehard_squeeze| 0| 100000| 100|0.24753753| PASSED
diehard_sums| 0| 100| 100|0.05653317| PASSED
diehard_runs| 0| 100000| 100|0.11453525| PASSED
diehard_runs| 0| 100000| 100|0.19585625| PASSED
diehard_craps| 0| 200000| 100|0.45638793| PASSED
diehard_craps| 0| 200000| 100|0.31591645| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.06850479| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.81649089| PASSED
sts_monobit| 1| 100000| 100|0.99831362| WEAK
sts_runs| 2| 100000| 100|0.47933569| PASSED
sts_serial| 1| 100000| 100|0.15918179| PASSED
sts_serial| 2| 100000| 100|0.01980393| PASSED
sts_serial| 3| 100000| 100|0.26391074| PASSED
sts_serial| 3| 100000| 100|0.93825883| PASSED
sts_serial| 4| 100000| 100|0.48042579| PASSED
sts_serial| 4| 100000| 100|0.94648402| PASSED
sts_serial| 5| 100000| 100|0.88404757| PASSED
sts_serial| 5| 100000| 100|0.63829590| PASSED
sts_serial| 6| 100000| 100|0.87264060| PASSED
sts_serial| 6| 100000| 100|0.99025369| PASSED
sts_serial| 7| 100000| 100|0.52913922| PASSED
sts_serial| 7| 100000| 100|0.20699735| PASSED
sts_serial| 8| 100000| 100|0.51858724| PASSED
sts_serial| 8| 100000| 100|0.93935828| PASSED
sts_serial| 9| 100000| 100|0.89045694| PASSED
sts_serial| 9| 100000| 100|0.97967948| PASSED
sts_serial| 10| 100000| 100|0.82805945| PASSED
sts_serial| 10| 100000| 100|0.94576847| PASSED
sts_serial| 11| 100000| 100|0.87463478| PASSED
sts_serial| 11| 100000| 100|0.41233150| PASSED
sts_serial| 12| 100000| 100|0.82320320| PASSED
sts_serial| 12| 100000| 100|0.64700388| PASSED
sts_serial| 13| 100000| 100|0.91421216| PASSED
sts_serial| 13| 100000| 100|0.71090170| PASSED
sts_serial| 14| 100000| 100|0.30674023| PASSED
sts_serial| 14| 100000| 100|0.67525020| PASSED
sts_serial| 15| 100000| 100|0.63952330| PASSED
sts_serial| 15| 100000| 100|0.55714580| PASSED
sts_serial| 16| 100000| 100|0.73460968| PASSED
sts_serial| 16| 100000| 100|0.69422309| PASSED
rgb_bitdist| 1| 100000| 100|0.22341428| PASSED
rgb_bitdist| 2| 100000| 100|0.08136192| PASSED
rgb_bitdist| 3| 100000| 100|0.55014870| PASSED
rgb_bitdist| 4| 100000| 100|0.14073467| PASSED
rgb_bitdist| 5| 100000| 100|0.51289672| PASSED
rgb_bitdist| 6| 100000| 100|0.57743763| PASSED
rgb_bitdist| 7| 100000| 100|0.84468115| PASSED
rgb_bitdist| 8| 100000| 100|0.91538369| PASSED
rgb_bitdist| 9| 100000| 100|0.63104431| PASSED
rgb_bitdist| 10| 100000| 100|0.79467241| PASSED
rgb_bitdist| 11| 100000| 100|0.87835683| PASSED
rgb_bitdist| 12| 100000| 100|0.31145148| PASSED
rgb_minimum_distance| 2| 10000| 1000|0.24538060| PASSED
rgb_minimum_distance| 3| 10000| 1000|0.06060245| PASSED
rgb_minimum_distance| 4| 10000| 1000|0.52854808| PASSED
rgb_minimum_distance| 5| 10000| 1000|0.24081642| PASSED
rgb_permutations| 2| 100000| 100|0.79575115| PASSED
rgb_permutations| 3| 100000| 100|0.97655238| PASSED
rgb_permutations| 4| 100000| 100|0.72826877| PASSED
rgb_permutations| 5| 100000| 100|0.47653591| PASSED
rgb_lagged_sum| 0| 1000000| 100|0.88292658| PASSED
rgb_lagged_sum| 1| 1000000| 100|0.83634521| PASSED
rgb_lagged_sum| 2| 1000000| 100|0.05969674| PASSED
rgb_lagged_sum| 3| 1000000| 100|0.49726026| PASSED
rgb_lagged_sum| 4| 1000000| 100|0.99815217| WEAK
rgb_lagged_sum| 5| 1000000| 100|0.60472621| PASSED
rgb_lagged_sum| 6| 1000000| 100|0.57097784| PASSED
rgb_lagged_sum| 7| 1000000| 100|0.80903695| PASSED
rgb_lagged_sum| 8| 1000000| 100|0.14512311| PASSED
rgb_lagged_sum| 9| 1000000| 100|0.91611538| PASSED
rgb_lagged_sum| 10| 1000000| 100|0.92420750| PASSED
rgb_lagged_sum| 11| 1000000| 100|0.60042568| PASSED
rgb_lagged_sum| 12| 1000000| 100|0.13617953| PASSED
rgb_lagged_sum| 13| 1000000| 100|0.24046263| PASSED
rgb_lagged_sum| 14| 1000000| 100|0.92188587| PASSED
rgb_lagged_sum| 15| 1000000| 100|0.28283582| PASSED
rgb_lagged_sum| 16| 1000000| 100|0.93668554| PASSED
rgb_lagged_sum| 17| 1000000| 100|0.84602342| PASSED
rgb_lagged_sum| 18| 1000000| 100|0.47539708| PASSED
rgb_lagged_sum| 19| 1000000| 100|0.91932322| PASSED
rgb_lagged_sum| 20| 1000000| 100|0.22697424| PASSED
rgb_lagged_sum| 21| 1000000| 100|0.86299916| PASSED
rgb_lagged_sum| 22| 1000000| 100|0.44319686| PASSED
rgb_lagged_sum| 23| 1000000| 100|0.49607458| PASSED
rgb_lagged_sum| 24| 1000000| 100|0.64071058| PASSED
rgb_lagged_sum| 25| 1000000| 100|0.67651856| PASSED
rgb_lagged_sum| 26| 1000000| 100|0.05264378| PASSED
rgb_lagged_sum| 27| 1000000| 100|0.52894581| PASSED
rgb_lagged_sum| 28| 1000000| 100|0.23036343| PASSED
rgb_lagged_sum| 29| 1000000| 100|0.08698878| PASSED
rgb_lagged_sum| 30| 1000000| 100|0.91367390| PASSED
rgb_lagged_sum| 31| 1000000| 100|0.50385001| PASSED
rgb_lagged_sum| 32| 1000000| 100|0.39512022| PASSED
rgb_kstest_test| 0| 10000| 1000|0.05304759| PASSED
dab_bytedistrib| 0| 51200000| 1|0.07108892| PASSED
dab_dct| 256| 50000| 1|0.06583399| PASSED
Preparing to run test 207. ntuple = 0
dab_filltree| 32| 15000000| 1|0.77425875| PASSED
dab_filltree| 32| 15000000| 1|0.10287529| PASSED
Preparing to run test 208. ntuple = 0
dab_filltree2| 0| 5000000| 1|0.64344940| PASSED
dab_filltree2| 1| 5000000| 1|0.13915721| PASSED
Preparing to run test 209. ntuple = 0
dab_monobit2| 12| 65000000| 1|0.55077431| PASSED
‘dieharder’ Conclusion
The total number of ‘dieharder’ ‘weak’ assessments was higher for /dev/urandom.
Turning your computer into a 1 Gbps random number generator
April 21, 2018
Earlier this year we launched our new product—SwiftRNG Pro—a hardware random number generator that can produce high quality random bytes at 200 megabits per second. If you are looking for a faster generation speed then you have two options: you can either buy expensive hardware that generates random bytes at higher rates, or you can try out the SwiftRNG software API clustering feature.
In this post we will show how to use five SwiftRNG Pro devices to turn your computer into a high quality hardware random number generation machine that can produce random bytes at a speed of 1 Gbps. The SwiftRNG API provides device cluster scalability and fail-over capabilities. With this, it is possible to use multiple SwiftRNG devices to additively increase the random number generation speed. This API feature seamlessly integrates multiple devices and uses them concurrently as a single stream of random data (Fig. 1).
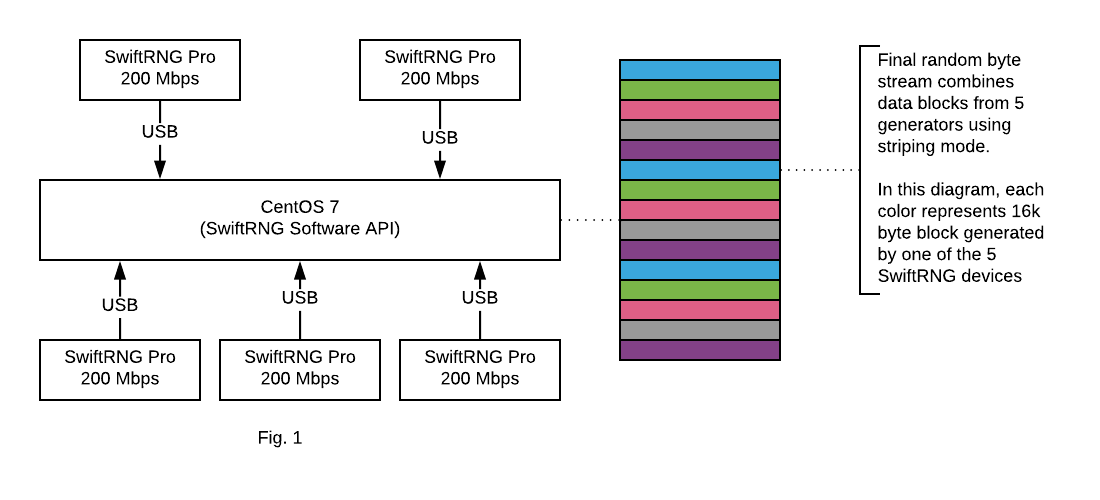
When working on your 1 Gbps HWRNG machine, your computer should meet the following requirements:
- A fast CPU with at least 4 cores. (We used a six core I7-8700 CPU at 3.2 GHz.)
- A mainboard that supports at least 5 USB HS ports (USB3 type is recommended for best results). We used ‘Gigabyte Ultra Durable Motherboard Z370 HD3P LGA 1151’
- Cent OS 7.
- 5 SwiftRNG Pro devices: each device should be plugged directly into a USB port available. Do not use USB hubs.
- SwiftRNG software utilities are built and available for CentOS from a command line.
To test your SwiftRNG Pro device cluster performance, download 60 GB of random bytes from the SwiftRNG cluster by entering the following in the command line:
swrng-cl -dd -fn STDOUT -cs 5 | dd bs=12000000 count=5000 iflag=fullblock of=/dev/null
The output may look like this (in the output below, 139 MB/s indicates that the download speed was around 1 Gbps):
5000+0 records in
5000+0 records out
60000000000 bytes (60 GB) copied, 431.234 s, 139 MB/s
To test the randomness quality of your SwiftRNG Pro device cluster, run the following in the command line:
swrng-cl -dd -fn STDOUT -cs 5 | dd bs=12000000 count=5000 iflag=fullblock | ent
The output may look like this:
5000+0 records in
5000+0 records out
60000000000 bytes (60 GB) copied, 1441.62 s, 41.6 MB/s
Entropy = 8.000000 bits per byte.
Optimum compression would reduce the size
of this 60000000000 byte file by 0 percent.
Chi square distribution for 60000000000 samples is 251.46, and randomly
would exceed this value 55.09 percent of the times.
Arithmetic mean value of data bytes is 127.4996 (127.5 = random).
Monte Carlo value for Pi is 3.141587391 (error 0.00 percent).
Serial correlation coefficient is 0.000002 (totally uncorrelated = 0.0).
SwiftRNG device integration use cases
April 20, 2018
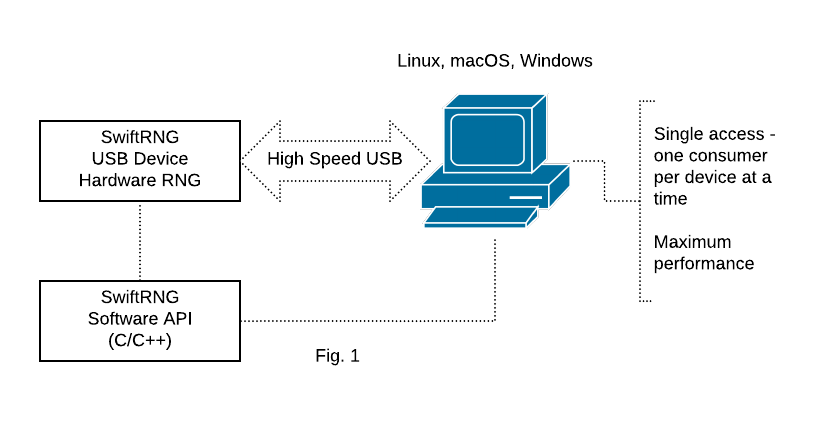
SwiftRNG device integration using the API on Linux, macOS and Windows
SwiftRNG Software API is the simplest way to integrate your C/C++ application source code with a SwiftRNG device for achieving maximum download speed and performance. When using this model (Fig. 1), additional internal device features become accessible such as: running on-demand device diagnostics, accessing the raw random byte stream, downloading frequency tables for each noise source or setting power profiles. When using this integration solution, only one application (consumer) will be accessing SwiftRNG device at a time.
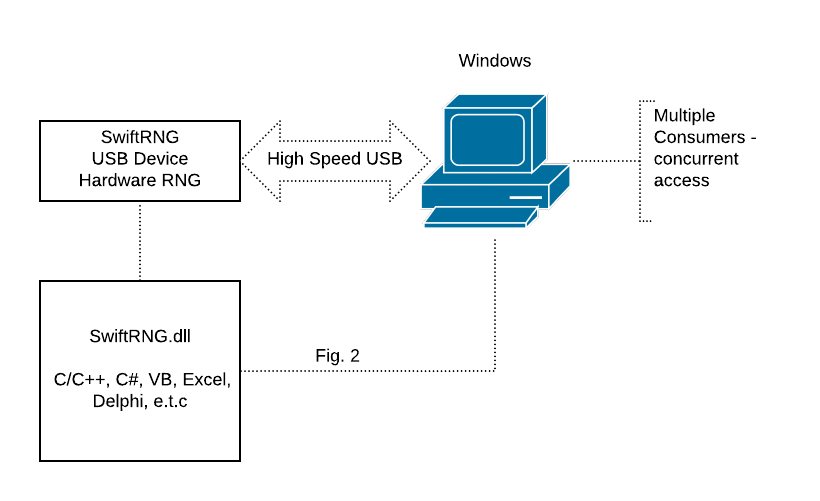
SwiftRNG device integration using SwiftRNG.dll on Windows
The supplied SwiftRNG.dll can be used to integrate SwiftRNG devices with applications that are developed to run on 32-bit or 64-bit Windows platforms (Fig. 2). The software kit contains source code examples that demonstrate how to use the DLL with C/C++ applications. You will also find source code examples on how to utilize the SwiftRNG.dll with languages such as C#, VB and Excel VB by visiting our documentation sections. The DLL will allow accessing the SwiftRNG random byte stream by multiple applications concurrently.
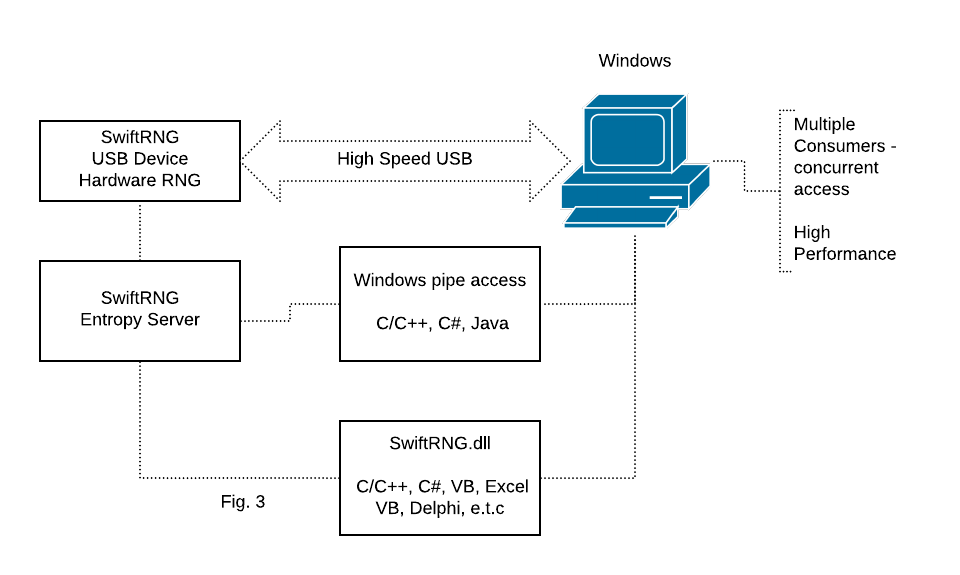
SwiftRNG device integration using Entropy Server on Windows
Entropy Server application is available for Windows and is used as an alternative way for distributing random bytes generated by a SwiftRNG device (Fig. 3). The SwiftRNG.dll can be used to access the server concurrently with maximum performance. Applications written in languages such as C/C++, C# and Java alternatively can access the Entropy Server directly, using a windows pipe without the use of the SwiftRNG dll.
SwiftRNG device integration using ‘swrandom’ kernel device module on Linux
The SwiftRNG Software Kit contains a Linux kernel module ‘swrandom’ that can be used to distribute random byte stream generated by a SwiftRNG device to any application that is capable to read from a file. The random byte stream generated can be concurrently accessible by consumer applications using device /dev/swrandom (Fig. 4). We recommend using this integration model on platforms such as Ubuntu, CentOS, RH in production environment.
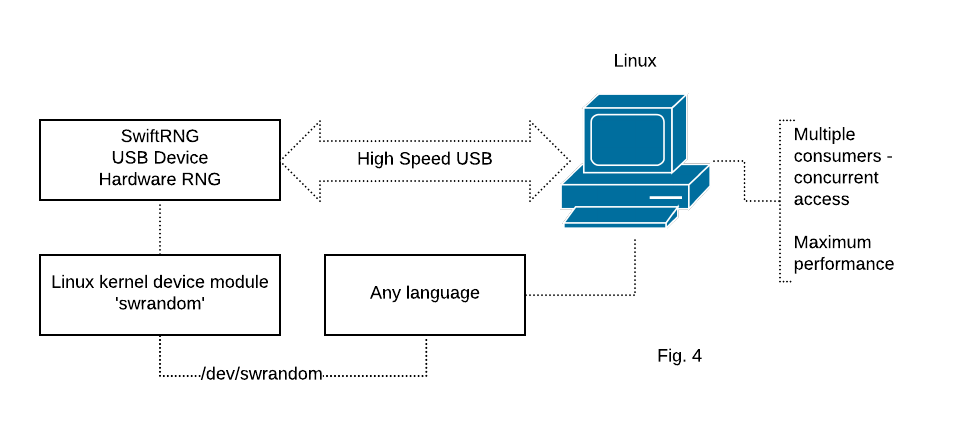
SwiftRNG device integration for feeding the entropy pool on Linux
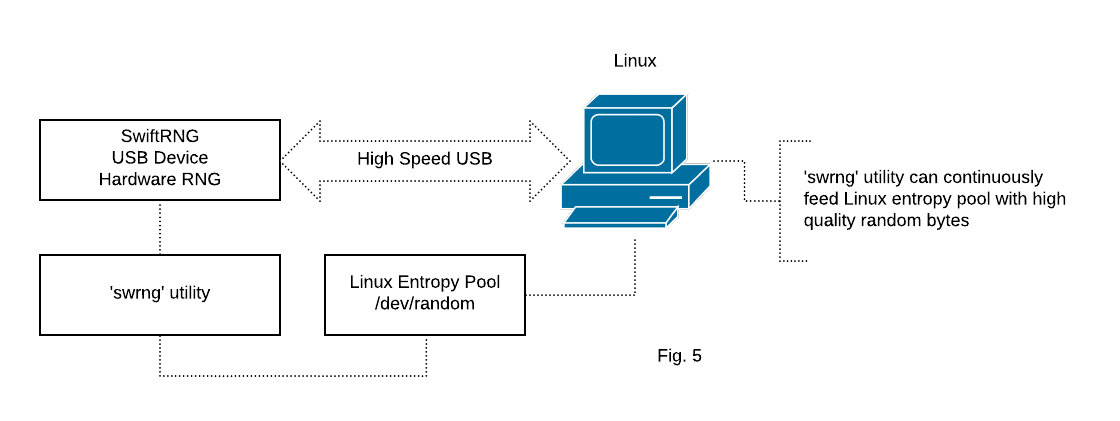
SwiftRNG Software kit provides a ‘swrng’ utility that can be used to feed the entropy linux pool ‘/dev/random’ with high quality random numbers generated by a SwiftRNG device (Fig. 5).
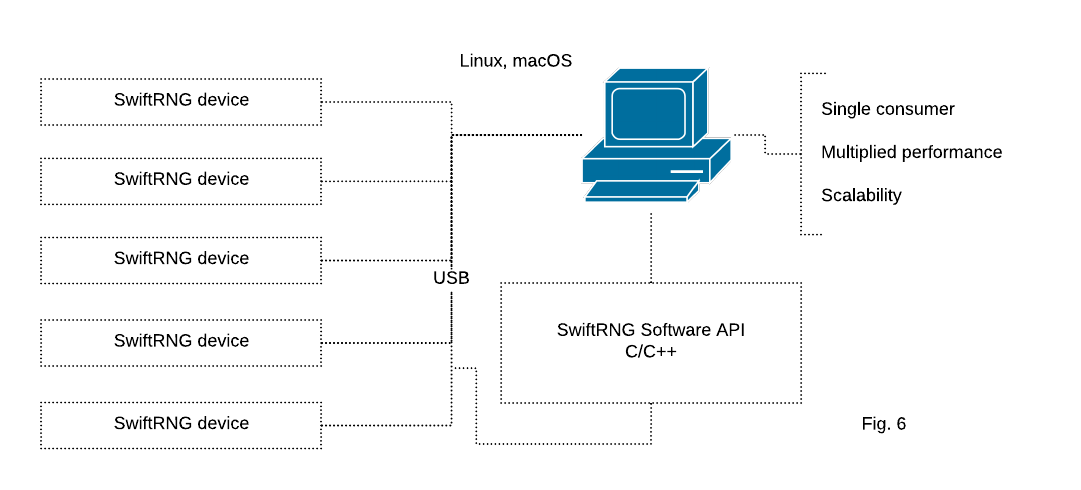
Using multiple SwiftRNG devices in a cluster with Linux and macOS
SwiftRNG API provides device cluster scalability and fail-over capabilities. With this, it is possible to use multiple SwiftRNG devices to additively increase the random number generation speed. This API feature seamlessly integrates multiple devices and uses them concurrently as a single stream of random data (Fig. 6). The feature is available when used with C/C++ applications and it is supported by SwiftRNG software utilities.
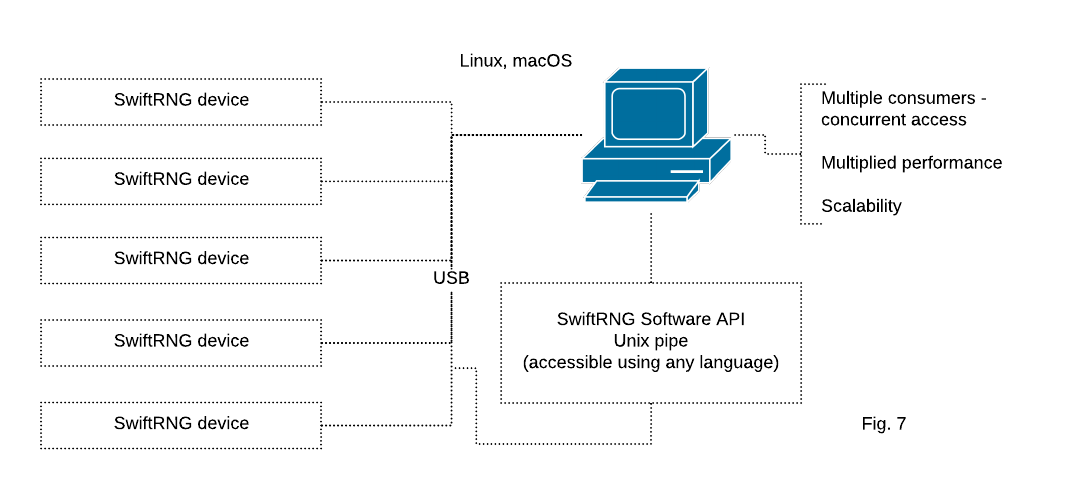
Using multiple SwiftRNG devices in a cluster utilizing Unix pipe on Linux and macOS
SwiftRNG software kit provides a utility for using a cluster of multiple SwiftRNG devices to additively increase the random number generation speed. The random bytes are distributed by a Unix pipe and can be concurrently accessed from any application with file access capabilities (Fig. 7).
Ambient temperature and EMF effects on SwiftRNG randomness
April 1, 2018
In this blog post, we attempt to answer the following question:
Can ambient temperature and EMF affect the outcome of SwiftRNG output results?
Overview
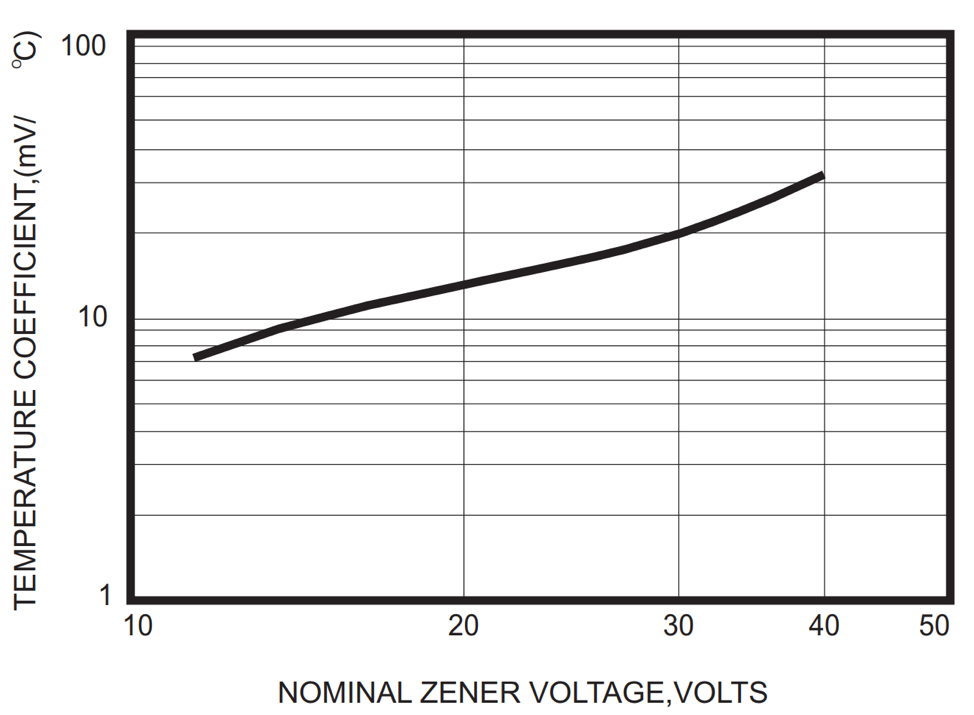
If you pull up technical datasheets of any commercially available Zener diode, you will find, among other technical characteristics, a “Temperature Coefficients” chart. This chart shows the correlation between the nominal Zener voltage and the temperature. We are interested only in Zener diodes with nominal voltages above 5–6 volts, which predominantly use the avalanche breakdown effect. In these Zener diodes, the temperature coefficient is positive. This means that the breakdown voltage will increase once the temperature increases.
In the chart below, we can see that when using Zener diode with nominal voltage of 15 V, the temperature coefficient is approximately 10 mV per degree Celsius. That also means that when the temperature increases by 100 °C (212 °F), the breakdown voltage will increase by 1 V. It is very unlikely that the temperature of the Zener diode used in SwiftRNG will ever increase by 100 °C. If the breakdown voltage increases by 1 V then it won’t deteriorate or make the random noise source less random or decrease the quality of the random output.
To help testing the influence of electromagnetic fields (EMF) on SwiftRNG output quality, we used an AM-10 meter. The acoustimeter AM-10 is a broadband meter that measures the EMF in the range of 200 MHz to 8 GHz. This covers the frequencies used by most modern communication systems in our modern everyday environment.
Experiments
We conducted three experiments to find out how the ambient temperature and EMF can influence the random outcome of Zener-based random noise sources in SwiftRNGs. The same SwiftRNG device was used for all experiments.
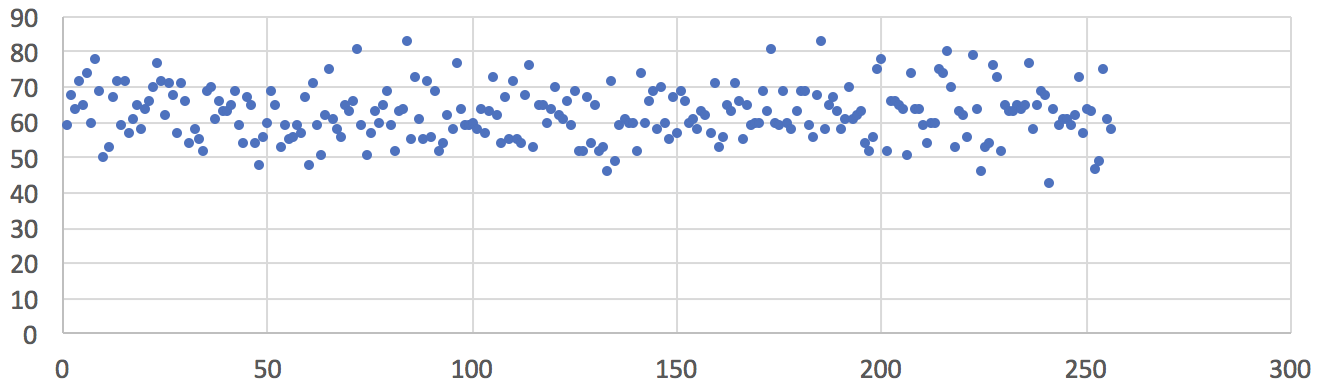
The first experiment was conducted when the ambient temperature was -8 °C (18 °F), the ambient average EMF was less than 1 µW/m², and the peak EMF was less than 0.02 V/m measured with the AM-10 Meter. The only way we could find a place with such low EMF level was by driving to the nearest park, away from streets, offices, and pedestrians that may use cell phones and Bluetooth devices. The chart below shows the uniform frequency distribution of 16,000 sampled random bytes (in the value range of 0 to 255) from a single Zener-based noise source. In addition, we collected 120 MB of raw data output from the SwiftRNG. No evidence of data quality degradation was found when testing this output with the ENT test for randomness.
Fig1: Frequency distribution of 16,000 random values sampled from one noise source. Ambient temperature –8 °C (18 °F), ambient average EMF less than 1 µW/m², peak EMF less than 0.02 V/m. Horizontal axis represents a converted random byte value. Vertical axis represents number of occurrences.
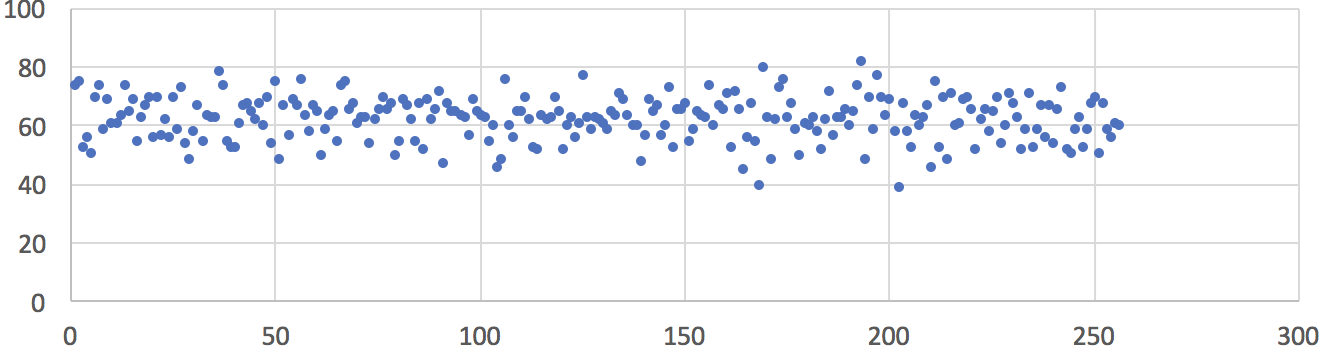
The second experiment was conducted when the ambient temperature was 24 °C (75 °F), the ambient average EMF was less than 1 µW/m² and the peak EMF was less than 0.02 V/m measured with AM-10 Meter. The chart below shows the uniform frequency distribution of 16,000 sampled random bytes (in the value range of 0 to 255) from a single Zener-based noise source. In addition, we collected 120 MB of raw data output from the SwiftRNG and could not detect any evidence of data quality degradation when testing with the ENT test.
Fig2: Frequency distribution of 16,000 random values sampled from one noise source. Ambient temperature 24 °C (75 °F), ambient average EMF less than 1 µW/m², peak EMF less than 0.02 V/m. Horizontal axis represents a converted random byte value. Vertical axis represents number of occurrences.
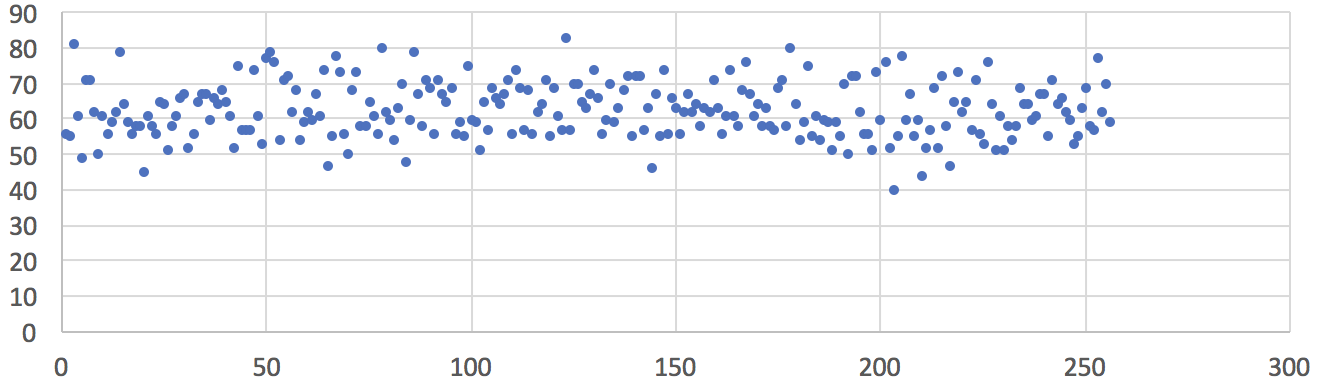
The third experiment was conducted for extreme conditions when the ambient temperature was 28 °C (82 °F), the ambient average EMF was less than 200 µW/m² and the peak EMF was less than 4 V/m measured with AM-10 Meter. Such EMF level can be found in the office in near proximity of WiFi routers or other radio communication devices. The chart below shows the uniform frequency distribution of 16,000 sampled random bytes (in the value range of 0 to 255) from a single Zener-based noise source. In addition, we collected 120MB of raw data output from the SwiftRNG and could not detect any evidence of data quality degradation when testing with the ENT test.
Fig3: Frequency distribution of 16,000 random values sampled from one noise source. Ambient temperature 28 °C (82 °F), ambient average EMF more than 200 µW/m², peak EMF at 4 V/m. Horizontal axis represents a converted random byte value. Vertical axis represents number of occurrences.
Conclusion
Based on our testing conducted with the ENT test for randomness, we did not find any evidence that ambient temperature and EMF can influence the outcome of SwiftRNG random output quality.
In depth: How SwiftRNG generates true random numbers
February 18, 2018
In the first installment of our SwiftRNG In Depth series, we will explore how each SwiftRNG device generates true random numbers from Zener diodes. The diagram below is a schematic representation of a SwiftRNG device in the top-half, and a host computer in the bottom-half. We will be going over the different parts of this diagram below.
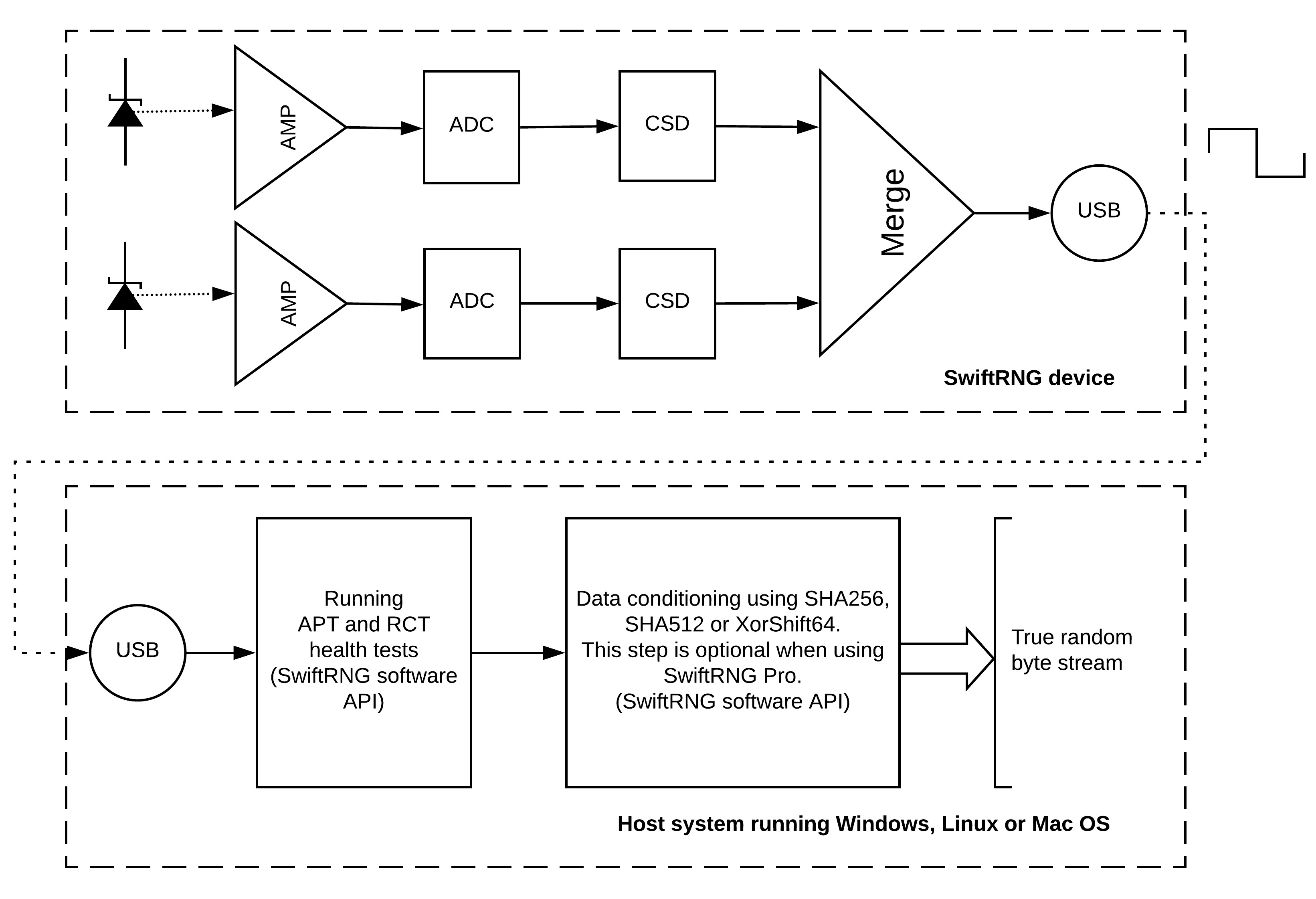
Step 1: Noise production
Each SwiftRNG contains two reverse-biased Zener diodes, which are shown in the top-left of the diagram. These Zener doides generate noise from the avalanche breakdown effect. The Zener diode is a semiconductor component. In other devices, Zener diodes are often used in DC circuits as voltage regulators or to provide voltage references.
The frequency range of the electrical noise generated by a Zener diode depends on the component manufacturer, breakdown voltage and physical dimensions. Depending on the diode, avalanche breakdown is observed at above 6-8 volts, and the electrical noise generated in such components is strong enough to be measured, and has the characteristics of randomness. This makes Zener diodes a candidate for a good noise source in hardware random number generators.
Avalanche diodes such as Zener diodes generate large quantities of radio frequency noise and are widely used for RF measurements. After extensively testing noise sources based on Zener diodes, we have found no evidence of any quality deterioration over time.
The following is a spectrum analyzer waterfall that was created by sampling the noise generated from a Zener diode used in SwiftRNG. The chart shows the magnitude of the noise signal versus frequency within the frequency range of 10 MHz to 54 MHz. It shows a smooth distribution of the frequencies of the noise.

Step 2: Noise amplification
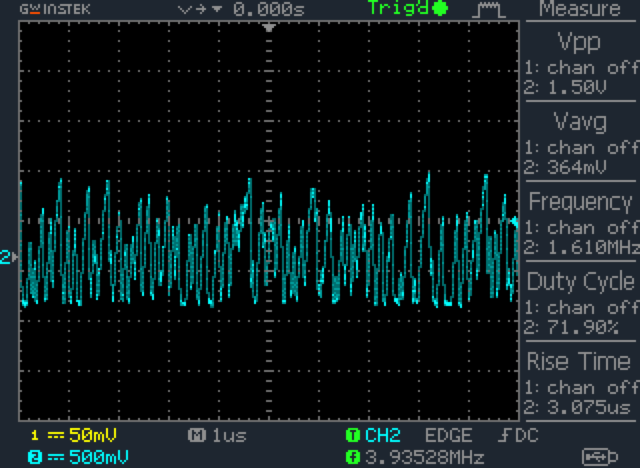
Each of the two Zener diodes is connected to an amplifier (labeled AMP in the diagram), which amplifies the electrical noise. At this point, the noise data is still in analog form.
The following plot was generated by an oscilloscope that measured the amplified random electrical analog signal generated by a Zener diode.
Step 3: Conversion to digital form
The result of noise amplification from each amplifier is then sent to an analog-to-digital converter (labeled as ADC in the diagram). The ADC converts the analog signal into a digital stream of random bytes. Each Zener diode, amplifier, and converter together form an independent noise source, and each SwiftRNG device contains two of these independent noise sources.
Step 4: Digitized value validation
Digitized random values from each noise source is then sent to a continuous self-diagnostics component (labeled as CSD in the diagram), which validates the random values. The component performes frequency analysis, and checks for deteriorations or malfunctions in the noise source. The result of this analysis is reported in the overall generator status code.
Step 5: Byte stream merge
The independent byte streams produced are then merged into one stream using logical XOR and shifting operations. The final random bytes produced by SwiftRNG Pro have excellent random characteristics, a very low BIAS and don’t require any additional whitening processing. This is shown in the component named ‘Merge’ in the diagram.
Step 6: USB transmission
The resulting bytes are transmitted to the host system using SwiftRNG software API through USB interface. A monitoring logic built into the software API of the SwiftRNG checks the quality of the final random bytes produced. This is done by continuously running Repetition Count tests and Adaptive Proportion tests, as specified by NIST Special Publication (SP) 800-90B.

Step 7: Post-processing
In the final step, the random bytes are fed to a conditional component by applying SHA256, SHA512 or XorShift64 post processing method. This data conditioning step is optional for SwiftRNG Pro.
The final bytes produced can be accessed with the supplied SwiftRNG software kit on Windows, Linux and macOS.
A new generator for a new year: The SwiftRNG Pro
January 1, 2018
2017 has been a wild ride, hasn’t it? It sure has been a big year in the digital world. More websites adopted HTTPS in 2017 than any other year, and people are more aware than ever of the security and privacy challenges faced by citizens and businesses alike. At the same time, it was the year the open internet faced the biggest obstacle with the repeal of Net Neutrality, and broadband privacy faced a major setback.
Here at TectroLabs, we released the SwiftRNG LE just over a year, making our unique true random number generating technology available to many more people at a lower price point. We have also released an updated version of our SwiftRNG model in 2017, bringing improved reliability and additional API features.
Since then, we have been working around the clock on a new generator that expands our family of SwiftRNG generators. To mark the new year 2018, we are so excited to announce our new device today: the SwiftRNG Pro. It has all of the awesome features of our SwiftRNG, but at 200 megabits per second, it has double the random number generation speed of the SwiftRNG, making it the world’s fastest USB-based random number generator. And with new device diagnostics capabilities, it is easier than ever to deal with possible issues.
We hope that you’ll consider the SwiftRNG Pro for generating true random numbers. It can be purchased starting today here, and full information is available on the main SwiftRNG Pro page.
SwiftRNG Version 1.2
September 10, 2017
We are announcing today a new revision of our SwiftRNG device. This revision, version 1.2, meets NIST SP 800-90B (second draft) requirements and includes the following improvements:
- Updated hardware and firmware components for bringing functional reliability and quality of resulting random data stream to a new level.
- Updated the device API and Software Kit with new commands for retrieving frequency tables of noise sources and for retrieving raw original byte stream data for each noise source. This transparency of raw entropy stream enables independent security testing and validation.
Available today, version 1.2 of SwiftRNG can be purchased here.
Edited September 10, 2017
SwiftRNG on Amazon
June 4, 2017
We are happy to announce that SwiftRNG and SwiftRNG LE are now both available for purchase through Amazon.com! The SwiftRNG can be found here, and SwiftRNG LE is available here.
SwiftRNG Software API cluster capability with Linux and OS X
April 8, 2017
We are announcing today an important update of the SwiftRNG Software Kit. Beginning with version 3.3, the SwiftRNG API contains device cluster scalability and fail-over capabilities. With this, it is possible to use multiple SwiftRNG devices to additively increase the random number generation speed. By doing so, the reliability of the cluster is increased. This new API feature seamlessly integrates multiple devices and uses them concurrently as a single stream of random data. The API will monitor the health of the cluster and will resize the cluster on-the-fly, allowing device swapping in real-time. This makes it possible to remove and add SwiftRNG devices in the middle of random number generation.
SwiftRNG software kit update brings cluster scalability and fail-over capabilities to the API
April 7, 2017
This week we released version 3.3 of the SwiftRNG software kit. This update adds device cluster scalability and fail-over capabilities to the SwiftRNG software API. With this, it is possible to use two or more SwiftRNG devices to additively increase the random number generation speed. By doing so, the reliability of the cluster is increased. This new API feature seamlessly integrates multiple devices and uses them concurrently as a single stream of random data. The API will monitor the health of the cluster and will resize the cluster on-the-fly, allowing device swapping in real-time. This makes it possible to remove and add SwiftRNG devices in the middle of random number generation.
For more information on how to use this feature, visit the SwiftRNG general documentation page. The new kit may be downloaded from our downloads page.
SwiftRNG Version 1.1
December 30, 2016
We are announcing today a new revision of our SwiftRNG device. This revision, version 1.1, contains the following improvements:
- Improved power consumption – SwiftRNG 1.1 uses up to 200 mA, down from 250 mA.
- Reduced operating temperature.
- Maximum ambient temperature is now 80 degrees Fahrenheit (26 degrees Celsius).
- Low power mode when idling — SwiftRNG 1.1 consumes less power when not in active use.
- Device cluster scalability and fail-over capabilities through the SwiftRNG software API on Linux and macOS.
Available today, version 1.1 of SwiftRNG can be purchased here.
If you are experiencing any problems with your SwiftRNG 1.0 and are under warranty, please contact us. We are able to replace your original device with a SwiftRNG revision 1.1 at no extra cost in most cases.
Edited June 4, 2017
Announcing SwiftRNG LE
December 29, 2016
We are happy to announce a lite edition of the of our SwiftRNG device: SwiftRNG LE. At an affordable price of $199 USD, SwiftRNG LE generates random numbers at 20 megabites per second, and consumes no more than 110 mA.
Like the standard edition, SwiftRNG LE has a length of just 7.9 cm and a weight of 21 grams. It can be used with just about any system, ranging from large-scale servers to the Raspberry Pi 2. And with a module provided by TectroLabs, setting it up is easy. Random numbers generated by SwiftRNG LE pass all statistical tests for randomness, including Diehard, DIeharder, NIST, and ENT.
SwiftRNG LE comes with software that makes it compatible with 64 and 32 bit Linux distributions, Windows, and macOS. It plugs into any computer with a USB port, and is appropriate for a wide range of uses, including research, simulations, and generating secure session and encryption keys.
SwiftRNG LE can be purchased here. Full information can be found on the main SwiftRNG page.
United States patent issued to TectroLabs for hardware number generation
October 29, 2016
TectroLabs, LLC, announced today the issuance to it by the United States Patent and Trademark Office of a patent that covers hardware random number generation technology.
US Patent 9,477,443 is for a method and apparatus of entropy source with multiple hardware random noise sources and continuous self-diagnostic logic.
The patent covers the technology in SwiftRNG, TL200, and TL100 hardware devices by TectroLabs that are used for generating true random numbers. SwiftRNG is a USB stick-sized device that generates random numbers at a rate of 100 megabits per second, faster than any other device of the same size.
Demand for hardware random number generators is growing rapidly as more companies seek to secure their applications and online presence. True hardware random number generators such as the SwiftRNG offer better security than pseudorandom software-based random number generators because they provide streams of random numbers that are unpredictable.
SwiftRNG now on Windows
February 28, 2016
With the new SwiftRNG Software Kit 2.1, we bring Windows support to your SwiftRNG! The new kit includes an updated swrng, that is fully compatible with Windows 8.1 and 10. With this new utility, Windows automatically installs the appropriate Windows certified driver without manual intervention when you plug in your SwiftRNG.
The kit was also recently updated with support for OS X. Download it today here!
SwiftRNG for OS X
February 14, 2016
We are happy to announce the availability of the SwiftRNG Software Kit 2.0, which includes a new software utility named swrng, which makes it possible to use SwiftRNG with OS X.
Download it today here!
Introducing SwiftRNG—The world’s fastest small-form random number generator
January 13, 2016

Today, we are unveiling SwiftRNG, the world’s fastest small-form random number generator. SwiftRNG is a USB stick sized device that generates random numbers at a rate of 100 megabits per second, faster than any other device of the same size.
With a length of just 7.9 cm and at 21 grams, SwiftRNG can be used with just about any system, ranging from large-scale servers to the Raspberry Pi 2. And with a module provided by TectroLabs, setting it up is easy. Random numbers generated by SwiftRNG pass all statistical tests for randomness, including Diehard, DIeharder, NIST, and ENT.
SwiftRNG comes with software that makes it compatible with 64 and 32 bit Linux distributions, including Ubuntu and CentOS. Support for Windows and OS X will be added in April 2016. It plugs into any computer with a USB port, and is appropriate for a wide range of uses, including research, simulations, and generating secure session and encryption keys. With software such as Virtio RNG, a single SwiftRNG is capable of generating random numbers to multiple guest instances in a cloud environment. With a speed of 100 megabits per second, it can be used to distribute one megabit per second to one hundred instances simultaneously.
SwiftRNG can be purchased at our online shop for $349. Learn more on the SwiftRNG page. Documentation is available online.
TectroLabs site refresh
January 3, 2016
Today, we’ve launched a new version of the TectroLabs site, built from the ground up with Jekyll. We hope the refresh will result in quicker page loads and an improved overall user experience. Along with the refresh, we’ve put up the latest version of our documentation online here, so it’s easily accessible from wherever you are. Please let us know what you think!
New software and documentation kits for TL200 and TL100
November 27, 2015
The Software & Documentation Kits for the TL200 and TL100 have been updated with new FTDI USB drivers for Linux and an FTDI setup executable for installing the certified drivers on Windows 10. They also contain various updates to the documentation.
The new kits may be downloaded from the downloads page.
Using TL100 and TL200 devices with an RNG daemon to feed the kernel’s random number entropy pool
May 24, 2015
TL100 and TL200 devices can now be used as entropy sources by using an RNG daemon. The daemon is available with the ‘rng-tools’ package on Linux, downloadable here.
Once the ‘tlrandom’ kernel module is successfully loaded, the entropy generated by the device can be used to feed the RNG daemon using the following command:
sudo rngd -r /dev/tlrandom
New ‘tlrandom’ kernel module for the TL200 and TL100
May 18, 2015
We are pleased to announce ‘tlrandom’, a new kernel module for Linux platforms. It can be used for interacting with the TL100 or TL200 devices. This module can be loaded by the kernel, upon which random bytes from the TL200 will be available for download from /dev/tlrandom.
You will be able to use ‘dd’ to download the random bytes using a command like this:
dd if=/dev/tlrandom of=download.bin bs=100 count=120000
The module has the ability to automatically detect when a TL100 or TL200 device is plugged in or unplugged from any USB port. Any application running in the user space should be able to open /dev/tlrandom and read random bytes generated by TL devices concurrently.
The new TL200 and TL100 Software & Documentation kits with ‘tlrandom’ are available to download here.
Updates to running the GetRND utility on Linux and OS X platforms
May 16, 2015
The TL200 and TL100 Software & Documentation kits have been updated with numerous fixes and additions. For Linux, an issue that could result in driver conflicts between a TL100 or TL200 device and kernel modules ‘ftdi_sio’ and ‘usbserial’ has been resolved.
For OS X, an issue that results in driver conflicts between the TL100 or TL200 device and kernel extension ‘AppleUSBFTDI’ has been resolved. This means that it is no longer necessary to disable OS X’s new D2XX driver to use the TL100 or TL200.
The update is available to download here.
TL200 ENT results from 280 GB of data
January 13, 2015
We have tested 280 GB of random bytes produced by a TL200 with ent, a command line utility that measures entropy. The statistical report is as follows:
Entropy = 8.000000 bits per byte. Optimum compression would reduce the size of this 289304498176 byte file by 0 percent. Chi square distribution for 289304498176 samples is 268.69, and randomly would exceed this value 50.00 percent of the times. Arithmetic mean value of data bytes is 127.5002 (127.5 = random). Monte Carlo value for Pi is 3.141577725 (error 0.00 percent). Serial correlation coefficient is 0.000001 (totally uncorrelated = 0.0).
More statistical reports of the TL200, including NIST, Diehard, and Dieharder, can be downloaded from our page about the TL200.
Introducing entropy feeder for TL200
January 13, 2015
We are pleased to announce Entropy Feeder (ef), a Linux command line utility that makes it even easier to feed random bytes produced by a TL200 to the Linux entropy pool. This utility is now a part of the TL200 Software & Documentation Kit, and can be downloaded here by TL200 users. Once downloaded, the command can be run by simply typing the following in a terminal:
sudo ./ef
When running the ef utility, the availability of random stream can be tested with this command:
sudo dd if=/dev/random of=/dev/null bs=1 count=1000000
The output of this command may look like this:
1000000+0 records in 1000000+0 records out 1000000 bytes (1.0 MB) copied, 8.41315 s, 119 kB/s
Download Entropy Feeder right now here.
New feature: random sequences of non-repeatable numbers
November 27, 2014
We’ve added a new feature to the TL200 that allows you to generate a random sequence of non-repeatable numbers. This random sequence is based on the true random numbers generated by the TL200, and is simple to generate using the GetRND utility. For example, we could use the following command to get a sequence of numbers 1 through 35 in a random order:
sudo ./getrnd -grs 1 35
This could result in the following output:
-- Beginning of random sequence -- 30 26 32 34 14 24 35 9 3 1 25 7 33 21 10 5 20 19 15 17 11 13 23 16 8 18 22 27 4 12 6 28 31 29 2 -- Ending of random sequence --
You can also limit the amount of numbers generated to less than the range. For example, you can choose to generate only the first five numbers of a random sequence of numbers from 1 through 10,000,000:
sudo ./getrnd -grs 1 10000000 5
This could result in the following output:
-- Beginning of random sequence -- 3830571 7697152 31227 8399071 3968532 -- Ending of random sequence --
Announcing the TL200
September 28, 2014
At TectroLabs, we strive to empower organizations and individuals to better meet their security needs with efficient and effective hardware and software solutions. Today, we are very pleased to announce the TL200, a big leap forward in our goal. The TL200 is a true hardware number generator that plugs directly into a USB port and generates numbers at a speed of 2.0 megabits per second. It is 40% faster and 60% lighter than the TL100 and contains new features such as selectable power profiles for different energy needs.

The TL200 has the same foundation as the TL100 and is fully compatible with the TL100, ensuring that applications built around the TL100 will be compatible with the TL200.
A visual comparison of bad and good hardware random number generators
July 4, 2014
Statistical tests are the best way to measure the quality of generated random numbers, but they’re not the only way. In fact, graphical outputs of random numbers allow people to visually inspect random numbers without relying on statistical outputs. Here, we compare the visual representations of numbers generated using a faulty random number generator, and true random numbers generated by a TL100.
In the following two images, try to see if you can spot any patterns in each image. Each pixel in the images represents one bit of random data, filled from left to right, line by line, from top to bottom.
Picture 1: This first image shows a bitmap graphical representation of numbers generated by a low-quality number generator. Notice that it is easy to observe long continuous horizontal black and white lines, which means that the generated bits are highly biased. Click on the image to view it in full size.
Picture 2: This second image shows a bitmap graphical representation of true random numbers generated by a TL100. In this image, visible patterns are difficult to spot, and it can be argued that there aren’t any. Click on the image to view it in full size.
tl100-trng-good-bitmap
As you can see, there is a clear difference between the two. Whereas the first image from the faulty hardware number generator has noticeable long lines from left to right, the second image from TL100 numbers shows black and white pixels mixed evenly, without any clear pattern.
Tutorial: How to feed the entropy pool in Linux
June 23, 2014
A TL100 or TL200 can be used to continuously feed the entropy pool of a computer running on a Linux operating system using the GetRND software utility. To do so, first plug in the device into your Linux computer and run the GetRND software utility. (Details on how to do this can be found in the Read Me file of the Software and Documentation Kit). Once you have successfully done so, simply run the following command from the command line:
sudo ./getrnd -dd -fep
The device will now continuously feed the entropy pool with true random bytes.
Tutorial: How to download random bytes to a file
June 22, 2014
A TL100 or TL200 can be used to download a specified or unlimited amount of random bytes and save it to a file on your disk using the GetRND software utility.
Note: The commands in this tutorial work for Linux and OS X operating systems. For Windows, replace ‘sudo ./getrnd’ with ‘getrnd.exe’ in all of the commands here.
Let us attempt to download 12 MB of to the file rnd.bin. To do so, first plug in the device into your computer and run the GetRND software utility. (Details on how to do this can be found in the Read Me file of the Software and Documentation Kit). Once you have successfully done so, simply run the following command from the command line:
sudo ./getrnd -dd -fn rnd.bin -nb 12000000
This command will create a file named rnd.bin if it doesn’t already exist, and download 12 MB of true random numbers to it. The command line may ask you to input your password. After that, wait a few seconds, and you should eventually see a message like this:
Processing request ... Completed in 51 seconds, speed: 229 KBytes/sec, blocks re-sent: 0
You may also choose to download random numbers continuously to a file. To download an unlimited amount of true random numbers to the file rnd.bin, run the following command from the command line:
sudo ./getrnd -dd -fn rnd.bin
This will continuously download true random numbers to rnd.bin, until you type Ctrl+C to abort.
Random numbers: An overview
March 20, 2014
In general, random number generation involves the use of a program or device referred to as a random number generator to generate a set of numbers that lack any discernible pattern and therefore are referred to as “random.” Just how random, and therefore how unpredictable, these random numbers are however, varies greatly from generator to generator.
Uses of random numbers
Humans have relied on randomness for thousands of years. Perhaps the most well known example in history is of Athenian democracy. In the fifth century BC, the legislative bodies of the government of Athens in Ancient Greece were made up of average citizens. Because of the strong support for direct democracy, Athenian citizens were selected at random to make up these bodies. Random selection was also used to select jurors for trials.
In modern times, juries are still selected at random, but the use of random number generation has also spread to countless other fields. In science, random numbers are used to create simulated data for economic models, climate change models, hurricane models, and even epidemiologist models. From simple models predicting the result of a number of coin tosses, to complex models simulating neutron transportation in nuclear fission, random numbers often play an important role.
Of course, random number generation is monumentally important in data security and encryption. Random number generators are used to create encryption keys, salts, and keyfiles for keeping data safely encrypted. If encryption keys are generated using a nonrandom approach, they can be predictable and easily determined, allowing just about anyone with the right expertise to decrypt and access your data.
Random number generation is also needed for lottery management systems and other random drawings. In some cases, unbiased random number generation is required by law, such as in random drug testing.
Reliability of random number generators
In 1969, the United States Selective Services System held a lottery to determine the order at which men would be called to military service in the Vietnam War based on birthdays. Each date from January 1 to December 31 was placed in a capsule, and the capsules were then mixed in a box, placed in a jar, and selected at random in a televised event. The order the dates were selected would be the order of drafting. However, it became apparent after the lottery that many more of the dates from November and December had lower rank numbers than other dates, and indeed, statistical analysis later showed that the results could not have been the result of an actually random process.
This example is relevant to answering the following questions: is a random number generator always as reliable as it seems, and if not, which ones can we trust to produce genuinely random numbers?
Pseudo versus true random number generation
Unfortunately, the previous example shows that random number generators are not always as accurate as they seem. In hindsight, there were important problems with the selection method in the 1969 draft lottery—notably, the capsules may not have been properly mixed in the box before being placed in the jar, leading to an unknown bias in selecting November and December dates.
Similarly, many random number generators used today are not actually random. These generators rely solely on computer algorithms to generate sequences of numbers that appear random and are called pseudorandom number generators (PRNGs). They produce sets of numbers from mathematical formulas that look random, but are actually periodic. If the starting point of a sequence is known, the exact same set of numbers can be generated over and over again. PRNGs are highly efficient, meaning they are able to produce large quantities of numbers quickly, but are by nature periodic and deterministic. Others can recreate the same set of numbers with the right starting information. This makes PRNGs unsuitable generators for many uses, including all types of data security, random sampling, and lotteries.
Other random number generators, known as true random number generators (TRNGs) use physical phenomena to generate sets of numbers. These generators do not rely solely on mathematical formulas. Instead, their source for random numbers can be all sorts of things, such as variations in a user’s mouse movement, atmospheric noise, or even radioactive decay.

